THE GOLDEN RATIO IN DESIGN

When a logo is to be created, a professional designer looks to the foundation on which all good design is crafted – The Golden Ratio, associated with the famous Italian mathematician, Leonardo Bonacci. He is known by his more popular name, Fibonacci. He birthed the theorem that certain numbers are equal to the sum of the preceding two numbers.

The Fibonacci Numbers start with the numbers 0 and 1. The first 20 Fibonacci numbers of sequence are: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181. (I’ll bet you’re looking at the number sequence and verifying that any number in the sequence after 0 and 1 is preceded by the numbers that precede it.

The importance is that as the numbers increase, the quotient between each successive pair of Fibonacci numbers is approximately 1.618. If you look at the opposite perspective, that quotient is approximately 0.618. This sequential proportion goes by many names: The Golden Ratio, The Golden Mean, Φ (Phi), and The Divine Proportion. The list of names goes on.  But stay close to this number (or its inverse). We’ll be referring to this number that represents proportion later in this blog article.

Now here is where Fibonacci gets the glory without some of the work.  Fibonacci is associated with the Golden Ratio, the Divine Proportion, and the other soubriquets. However, it was the Greek Mathematician, Euclid who first started confecting the concept of the Golden Ratio a/k/a “Extreme and Mean Ratio.” This concept was then picked up by an Italian Mathematician Luca Pacioli, a Franciscan Friar who collaborated here and there with Leonardo DaVinci. Pacioli is the gentleman who created the “Divine Proportion” concept associated with Fibonacci.  But first, let’s get into how these really smart gentlemen brought us to the concept of the Golden Rectangle.

In geometry, a golden rectangle is a rectangle whose side lengths are in the golden ratio, approximately 1.618.  (There’s that number we were talking about earlier!). Now let’s take a look at how these Fibonacci numbers build a rectangle that professional designers use.

The rectangle starts with a pair of small squares that represent the number 1. Now we add a second square representing the number 2 whose single side matches the length of the two small squares carrying the number 1. Now, let’s add another square that represents the number 3 whose side is equal to the combination of the number 2 and the pair of squares representing the number 1. We’ll add yet another square, again matching the side of the previously attached squares that represents the number 5. We keep repeating this sequential process of growing the rectangle until we have a rectangle of the substantial size necessary to build the graphic design. See the diagram below.

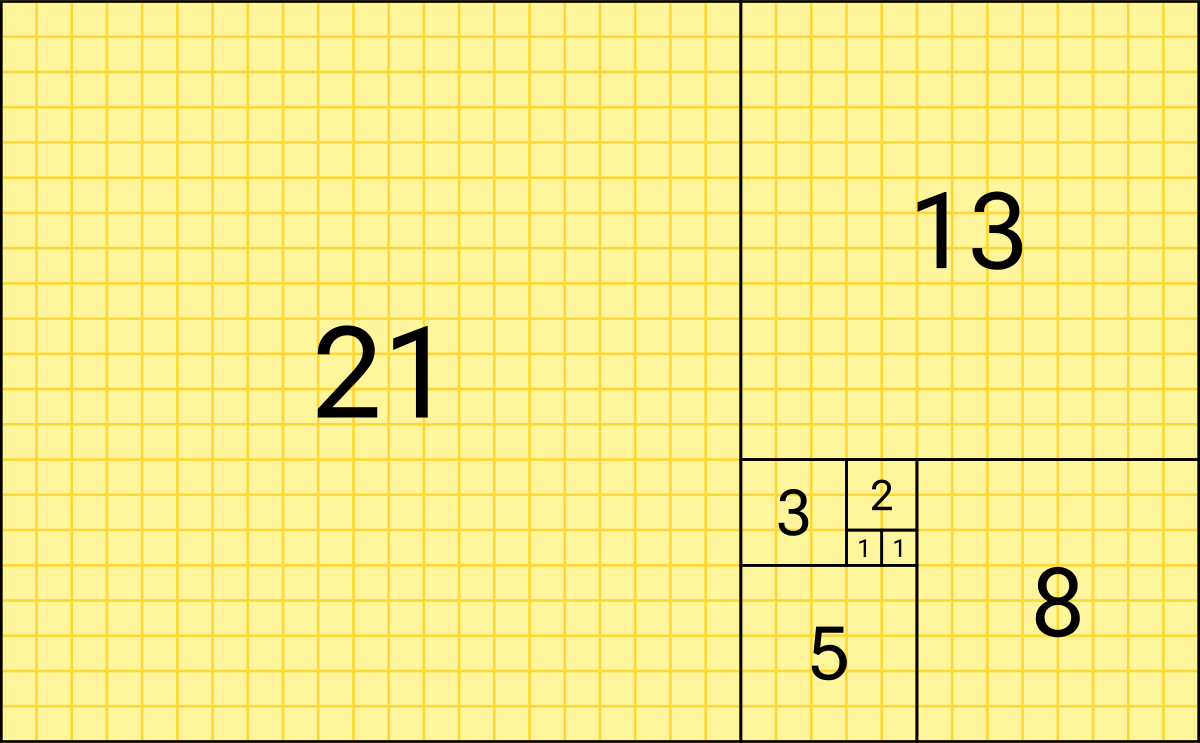
Now let’s add more intrigue and interest. You’re probably noticing the conspicuous spiral overlayed on the constructed rectangle. This is where the fun part comes in. If we place in each of those squares a 90 degree arc, we can connect them and create a spiral born upon the Fibonacci numbers sequence.  How cool is that??

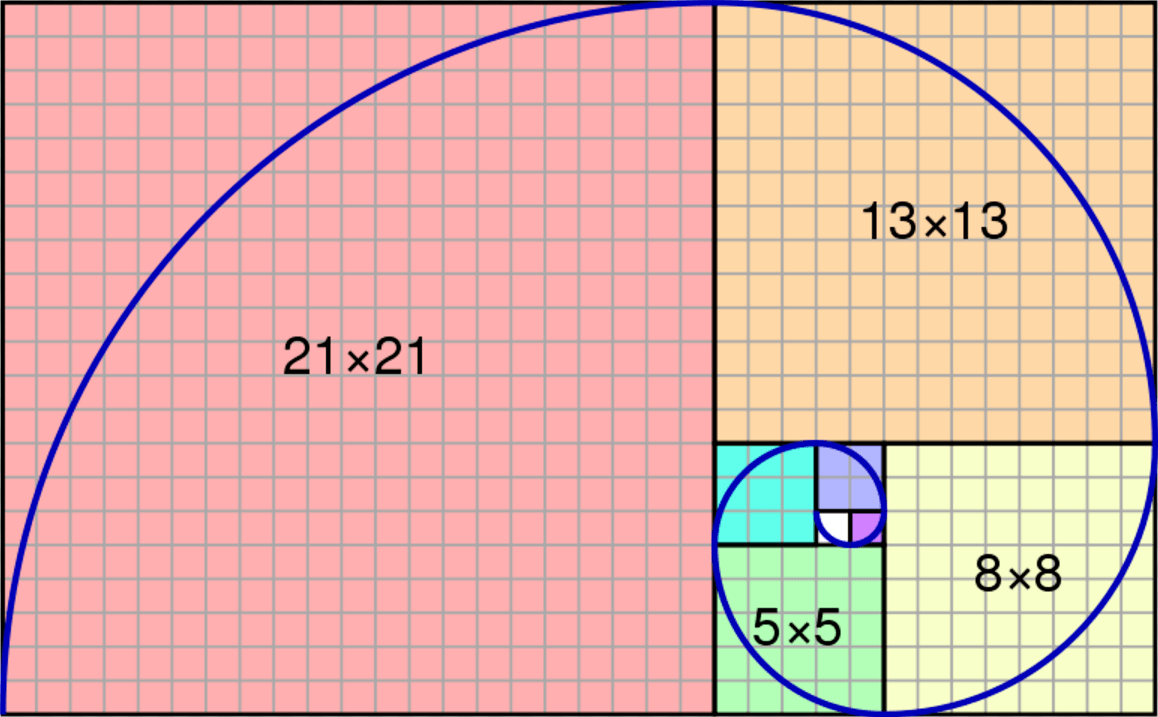
The rule is a rather fascinating subject worth reviewing in length.  However, let’s see how it applies to nature first. Then we shall discover at how it applies in design.

Take a look in your garden.  Buttercups have 5 petals; lilies and iris have 3 petals; some delphiniums have 8; corn marigolds have 13 petals; some asters have 21 whereas daisies can be found with 34, 55 or even 89 petals.  While the Golden Ratio doesn’t account for every structure or pattern in the universe, its presence cannot be discounted. Now get a load of the patterns in nature that match the spiral:

In our next post, we will review how the golden ratio is used in architecture and other man-made designs.